Musterbildung in einfachen Systemen

08.02.2015
c++, mathematik, python

Im vergangenen Sommer habe ich mit einem Kollegen zusammen an der Uni Münster einen Einführungskurs in die Programmiersprache Python gehalten, in dem die Teilnehmer insbesondere Grundlagen der numerischen Programmierung mit dieser Sprache gelehrt bekommen haben. Zu der Zeit bin ich mehr zufällig auf das Paper von J. E. Pearson (1993) gestoßen, in dem ein mathematisches Modell für Musterbildung in biologischen Systemen vorgestellt wird das trotz seiner relativen Einfachheit in der Lage ist, eine Vielzahl komplexer Dynamiken zu erzeugen. Da die Implementierung dieses Modells mit den im Rahmen des Kurses erworbenen Kenntnissen möglich ist, habe ich es motivierendes Beispiel am Ende vorgestellt. Ein paar Monate vergingen seitdem, bis ich diese Woche über einen Artikel bei Spiegel online gestolpert bin, der ein Paper (Stoop et al., 2014) zur mathematischen Modellierung von Musterbildungsprozessen auf elastischen Oberflächen beschreibt. Da die darin präsentierten Bilder starke Ähnlichkeiten mit meinen eigenen Simulationen aufweisen habe ich mich kurzerhand entschieden, einen Artikel über mein Programm zu schreiben.

Modell-Grundlagen und numerischer Ansatz

Dieser Abschnitt widmet sich der Darstellung von Modellierung und Grundlagen der numerischen Behandlung und ist für die mathematisch versierten Leser meines Blogs gedacht. Wer sich lediglich für die schicken Bilder und Videos interessiert kann auch gleich zum nächsten Abschnitt springen.

Das in Pearsons Paper "Complex Patterns in a Simple System" vorgestellte Modell basiert auf der Reaktion zweier unterschiedlicher Chemikalien, deren Konzentrationen mit $U(t)$ und $V(t)$ bezeichnet werden soll. Die grundlegenden chemischen Reaktionen sehen wie folgt aus: $$ \begin{align*} U + 2V &\to 3V \\ V &\to P \end{align*} $$ Anschaulich bedeutet dies, dass ein Teil der Substanz $U$ mit zwei Teilen von $V$ zu drei Teilen $V$ reagiert, während $V$ selbst zu einem weiteren Produkt $P$ zerfällt. Man nennt daher $U$ auch den Aktivator, weil dieser Stoff die Reaktion erst ermöglicht. Klar ist auch, dass $U$ ständig nachgefüllt werden muss wenn man die Reaktion am Laufen halten möchte.

Aus diesen Reaktionsgleichungen kann man nun ein mathematisches Modell für die Konzentrationen $U(t)$ und $V(t)$ ableiten. Dies führt zu folgendem System von partiellen Differentialgleichungen: $$ \begin{align*} \partial_t U(t) &= D_U \Delta U(t) - U(t) V^2(t) + F(1 - U(t)) \\ \partial_t V(t) &= D_V \Delta V(t) + U(t) V^2(t) - (F+k) V(t) \end{align*} $$ zusammen mit periodischen Randbedingungen. Die Parameter sind die Diffusionskonstanten $D_U, D_V$, die Fütterungsrate $F$ und die Reaktionsrate $k$ der zweite Reaktion relativ zur ersten. Wie man sieht handelt es sich um ein gekoppeltes System von Reaktions-Diffusionsgleichungen. Das System ist numerisch sehr stabil, so dass ein einfaches explizites Euler-Verfahren zur Zeitdiskretisierung zusammen mit finiten Differenzen für die Ortsableitungen ausreichend sind, um die Simulationen durchzuführen. Die Verwendung von expliziten Zeitschrittverfahren hat den Vorteil, dass man keine umständlichen Ansätze zum Entkoppeln machen muss. Als Schrittweiten kann man sowohl $\Delta t$ als auch $\Delta h$ auf 1 setzen, als Rechengebiet verwenden wir $[0,N]^2$ für natürliche Zahlen $N$, typischerweise etwa 256 oder 512. Für die Simulationen wurden die Diffusionskonstanten fixiert, während die Fütterungsrate F und die Reaktionsrate k variiert werden konnten. Für die Bilder und Videos wurde das Konzentrationsprofil $V(t)$ benutzt.

Simulationsergebnisse

Da ich mit der Simulationsgeschwindigkeit des ursprünglichen Python-Programms nicht zufrieden war habe ich mich entschieden, es in C++ mit dem Qt-Framework neuzuschreiben. Der Quellcode beider Programme findet sich auf meinem Github-Account unter github.com/michaelschaefer/grayscott. Die hier vorgestellten Ergebnisse wurden mit der C++-Version erstellt, die wie folgt aussieht: 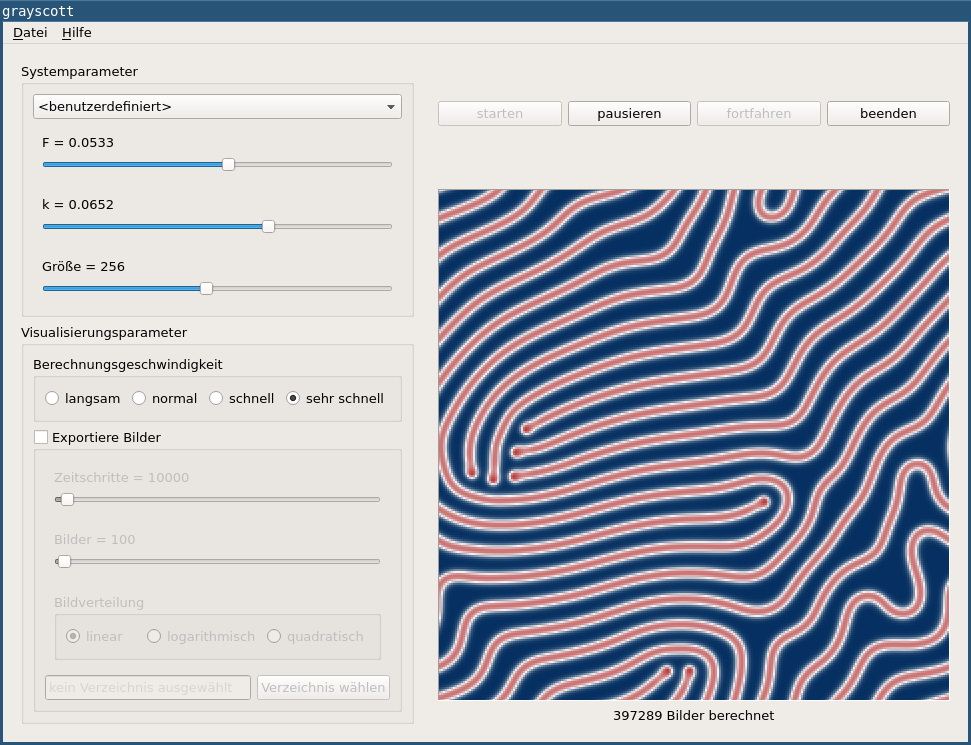In dem Programm lassen sich die relevanten Modell-Parameter und die Auflösung der Bilder variieren. Zusätzlich können Sequenzen von Einzelbildern automatisch auf Festplatte gespeichert werden, so dass man mit geeigneten Tools dann daraus Videos zusammensetzen kann. Obwohl das Verhalten des System sehr komplex auf Veränderungen der Parameter reagiert, lassen sich doch grob drei Kategorien unterscheiden die im Folgenden zusammen mit entsprechenden Simulationsergebnissen präsentiert werden. Durch Klicken auf das Bild gelangt man zum zugehörigen Video.

• Bakterien-artige Muster (sogar mit Zellteilung!), die aus einzelnen, sich nicht oder kaum bewegenden Punkten bestehen (F=0,035, k=0,065, N=512. Videogröße: 2,4MB)
• Fingerabdruck-artige Muster, die aus vielen verschlungenen Linien bestehen (F=0,035, k=0,06, N=512. Videogröße: 2,5MB)
• chaotische Muster, in denen ständig neue Punkte entstehen und wieder verschwinden (F=0,02, k=0,055, N=512. Videogröße: 8,9MB)

Als zusätzliches Gimmick habe ich eine Art Karte des Modells auf folgende Weise erstellt: Zunächst wurden zu verschiedenen Werten der beiden Parameter F und k Simulationen laufen gelassen und nach einiger Zeit für die jeweilige Dynamik (hoffentlich) repräsentative Bilder gespeichert. Am Ende wurden all diese einzelnen zu einem großen Bild, der Karte, zusammengefügt. Insgesamt wurden 81 verschiedene Werte für F und 41 für k verwendet, so dass die gesamte Karte aus 3321 verschiedenen Bildern besteht. Die Berechnungen nahmen auf einem Mehrprozessor-System einige Stunden in Anspruch. Das Resultat ist trotz JPEG-Kompression etwa 3,6MB groß, so dass ich das Bild hier nicht direkt einbinden möchte sondern lediglich verlinke. Der F-Wert ist in jeder Zeile konstant, während der k-Wert entlang der Spalten gleich bleibt.